Izokosta
Název této křivky se skládá ze dvou slov. Konkrétně IZO = stejný a COST = náklady. Význam této křivky je pak nasnadě, tedy křivka zobrazující stejné náklady. Využívá se především v ekonomické teorii a při stavování optimálního využití kapitálu ve vztahu k produkci.
Jedná se o vyjádření všech možných kombinací dvou vstupů, které může firma nakoupit při jejich stanovených cenách a při dané výši peněz. Řečeno jinými slovy, jedná se o všechny maximálně dostupné množstevní kombinace 2 výrobních faktorů při daném objemu nákladů.
Na obrázku níže vidíte izokostu (přímka) rovnou společně s izokvantou (křivka) v grafu dvou výrobních faktorů, konkrétně K – kapitál a L – práce.
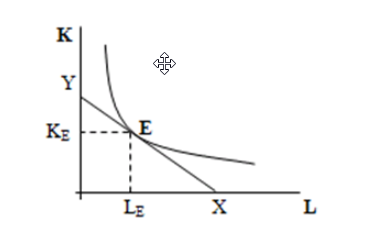
Bod Y se získá tak, že celkový objem stanovených nákladů (rozpočet) podělíme cenou výrobního faktoru na svislé ose (cenou kapitálu). Bod X získáme analogicky podělením stanovených nákladů cenou jednotky práce.
Tyto body symbolizují maximální dostupné množství jednoho výrobního faktoru při nulovém využití druhého.
Z grafu je rovněž patrný poměr (v závislosti na sklonu křivky), v jakém lze jeden výrobní faktor vyměňovat za druhý, aby byl stále plně vyčerpán. Tento směnný poměr lze snadno vypočíst podělením ceny VF na horizontální ose cenou VF na ose vertikální.
Jak se změní izokosta při změně ceny např. práce?
Takto by izokosta rotovala kolem bodu Y. Jestliže by se cena práce zvýšila, izokosta by protínala vodorovnou osu blíže k nule. Pokud by se cena práce snížila, izokosta by ji protínala samozřejmě dále od počátku os. Analogicky při změně ceny kapitálu.
Jak se změní izokosta při změně rozpočtového omezení?
V tomto případě se nemění sklon izokosty, ale celá se posouvá. Pokud bychom zvýšili rozpočet, tak se posune od průsečíku obou os a naopak, pokud bychom rozpočet omezili.
Souvislosti s izokvantou
Izokvanta vyjadřuje maximální množství, které může firma při použití daného množství dvou VF vyprodukovat. V bodě E se střetávají izokvanta a izokosta. Bod E je maximální množství, které lze při daných nákladech, dostupných zdrojích a dané produktivitě vyrobit s minimálním množstvím nákladů.